某企业设计了一款成本为20元/件的工艺品，并投放市场试销。通过市场调查，获得了销售单价（单位：元/件）与每天销售量（单位：件）之间的对应数据（数据表略）。本文基于调查数据，通过建立函数模型，分析销售单价与销售量的关系，并求解使每天利润最大的最优定价及相应的最大利润。

一、销售单价与销售量的函数关系分析

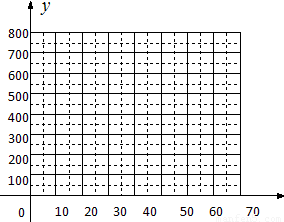
将数据表中各对（x，y）值（其中x表示销售单价，y表示每天销售量）作为点的坐标，在平面直角坐标系中描点。观察散点图可以发现，这些点大致分布在一条直线上，因此可以初步判断y是x的一次函数，即销售量与销售单价之间存在线性关系。

设函数关系式为：y = kx + b（k，b为常数，且k≠0）。

为了求出具体的函数关系式，我们选取数据表中的两组对应值（例如，当x=30时，y=500；当x=40时，y=400）代入方程，建立方程组：

500 = 30k + b … (1)
400 = 40k + b … (2)

用方程(2)减去方程(1)，得：

-100 = 10k
解得：k = -10
将k = -10代入方程(1)，得：
500 = 30 * (-10) + b
500 = -300 + b
解得：b = 800

因此，所求的函数关系式为：y = -10x + 800。

为了验证模型的准确性，可以将其他数据组代入此关系式进行检验。例如，当x=50时，计算得y = -1050 + 800 = 300，与调查数据相符；当x=60时，y = -1060 + 800 = 200，亦相符。这证实了y = -10x + 800能较好地反映该工艺品销售量随单价变化的规律。

二、利润最大化分析

已知每件工艺品的成本为20元。设销售单价为x元/件（x > 20），每天销售y件。

则每天的总销售收入（销售总价）为：x y 元。
每天的总成本为：20 y 元。

根据题意，利润（记为W）等于销售总价减去总成本，即：
W = x y - 20 y
= (x - 20) * y

将前面得到的函数关系式 y = -10x + 800 代入上式，得到利润W关于销售单价x的二次函数：
W = (x - 20) * (-10x + 800)
= -10x² + 800x + 200x - 16000
= -10x² + 1000x - 16000

这是一个开口向下的二次函数（因为二次项系数-10 < 0），其图像是一条开口向下的抛物线，函数存在最大值。

求最大利润及对应的销售单价，有两种常用方法：

方法一：配方法
W = -10x² + 1000x - 16000
= -10(x² - 100x) - 16000
= -10[(x² - 100x + 2500) - 2500] - 16000
= -10(x - 50)² + 25000 - 16000
= -10(x - 50)² + 9000

方法二：利用顶点坐标公式
对于二次函数 W = ax² + bx + c (a≠0)，当 x = -b/(2a) 时，函数取得最值。
此处 a = -10, b = 1000, c = -16000。
∴ 当 x = -1000 / (2 (-10)) = -1000 / (-20) = 50 时，W取得最大值。
最大值为：W_max = -10(50)² + 1000*50 - 16000 = -25000 + 50000 - 16000 = 9000。

结论：
（1）销售量y与销售单价x的函数关系式为：y = -10x + 800。
（2）当销售单价定为50元/件时，工艺厂试销该工艺品每天获得的利润最大，最大利润是9000元。

三、市场意义与策略建议

本分析表明，该工艺品的市场需求对价格较为敏感，单价每增加10元，日均销售量将减少100件。企业并非定价越高利润越大，而是存在一个最优价格点（50元）。在此价格下，企业能实现日均利润9000元。建议企业在试销阶段可采用50元/件的定价策略以最大化短期利润，同时持续关注市场反馈和成本变化，为长期定价和产量规划提供依据。